Nested loops

A more difficult, but also very interesting case to parallelize, is the nested loops.

We want to be able to transform code like

loop while $i \in [0;9]$


loop while $j \in [0;9]$

				$A[i,j] \gets B[i,:] \cdot C[:,j]$

				$j \gets f(j)$


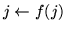
end

		$i \gets g(j)$


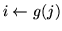
end

into

loop while $i \in [0;4]$


loop while $j \in [0;9]$

				$A[i,j] \gets B[i,:] \cdot C[:,j]$

				$j \gets f(j)$


end

		$i \gets g(j)$


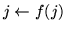
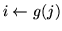
end


loop while $i \in [5;9]$


loop while $j \in [0;9]$

				$A[i,j] \gets B[i,:] \cdot C[:,j]$

				$j \gets f(j)$


end

		$i \gets g(j)$


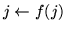
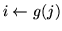
end

This would lend itself well to the sequence parallelizer, since we have two independent sets of nested loops.

Both loop structures use the $B$ and $C$ variables, but they don't touch them. The two structures touch two different subsets of $A$, so they really can be parallelized and run independently of each other.

This parallelization might not be as hairy to implement, as a first look on the wanted transformation could suggest.

Actually this parallelization is not much different from the core of the aforementioned instruction expansion. The only difference is the complexity of our function $f(\cdot)$, but the fact that we at all times work with sets of dependencies should make the actual complexity or size of some part of the code something we don't worry about.

Although this parallelization is not yet implemented, it may already be implemented partially. Because especially the dependency checking (which is the same dependency checking used in all parallelizers, since dependency checking is implemented in the opcode definitions, not in the parallelizers) is not yet completely implemented, we currently assume some dependencies that are actually not there. This makes the parallelizers work correctly (but not optimally) until I get the dependency checking routines completed.